티스토리 뷰
문제 설명
게임 개발자인 베로니는 개발 연습을 위해 다음과 같은 간단한 카드 짝 맞추기 보드 게임을 개발해 보려고 합니다.
게임이 시작되면 화면에는 카드 16장이 뒷면을 위로하여 4 x 4 크기의 격자 형태로 표시되어 있습니다. 각 카드의 앞면에는 카카오프렌즈 캐릭터 그림이 그려져 있으며, 8가지의 캐릭터 그림이 그려진 카드가 각기 2장씩 화면에 무작위로 배치되어 있습니다.
유저가 카드를 2장 선택하여 앞면으로 뒤집었을 때 같은 그림이 그려진 카드면 해당 카드는 게임 화면에서 사라지며, 같은 그림이 아니라면 원래 상태로 뒷면이 보이도록 뒤집힙니다. 이와 같은 방법으로 모든 카드를 화면에서 사라지게 하면 게임이 종료됩니다.
게임에서 카드를 선택하는 방법은 다음과 같습니다.
- 카드는 커서를 이용해서 선택할 수 있습니다.
- 커서는 4 x 4 화면에서 유저가 선택한 현재 위치를 표시하는 "굵고 빨간 테두리 상자"를 의미합니다.
- 커서는 [Ctrl] 키와 방향키에 의해 이동되며 키 조작법은 다음과 같습니다.
- 방향키 ←, ↑, ↓, → 중 하나를 누르면, 커서가 누른 키 방향으로 1칸 이동합니다.
- [Ctrl] 키를 누른 상태에서 방향키 ←, ↑, ↓, → 중 하나를 누르면, 누른 키 방향에 있는 가장 가까운 카드로 한 번에 이동합니다.
- 만약, 해당 방향에 카드가 하나도 없다면 그 방향의 가장 마지막 칸으로 이동합니다.
- 만약, 누른 키 방향으로 이동 가능한 카드 또는 빈 공간이 없어 이동할 수 없다면 커서는 움직이지 않습니다.
- 커서가 위치한 카드를 뒤집기 위해서는 [Enter] 키를 입력합니다.
- [Enter] 키를 입력해서 카드를 뒤집었을 때
- 앞면이 보이는 카드가 1장 뿐이라면 그림을 맞출 수 없으므로 두 번째 카드를 뒤집을 때까지 앞면을 유지합니다.
- 앞면이 보이는 카드가 2장이 된 경우, 두개의 카드에 그려진 그림이 같으면 해당 카드들이 화면에서 사라지며, 그림이 다르다면 두 카드 모두 뒷면이 보이도록 다시 뒤집힙니다.
- [Enter] 키를 입력해서 카드를 뒤집었을 때
"베로니"는 게임 진행 중 카드의 짝을 맞춰 몇 장 제거된 상태에서 카드 앞면의 그림을 알고 있다면, 남은 카드를 모두 제거하는데 필요한 키 조작 횟수의 최솟값을 구해 보려고 합니다. 키 조작 횟수는 방향키와 [Enter] 키를 누르는 동작을 각각 조작 횟수 1로 계산하며, [Ctrl] 키와 방향키를 함께 누르는 동작 또한 조작 횟수 1로 계산합니다.
다음은 카드가 몇 장 제거된 상태의 게임 화면에서 커서를 이동하는 예시입니다.
아래 그림에서 빈 칸은 이미 카드가 제거되어 없어진 칸을 의미하며, 그림이 그려진 칸은 카드 앞 면에 그려진 그림을 나타냅니다.
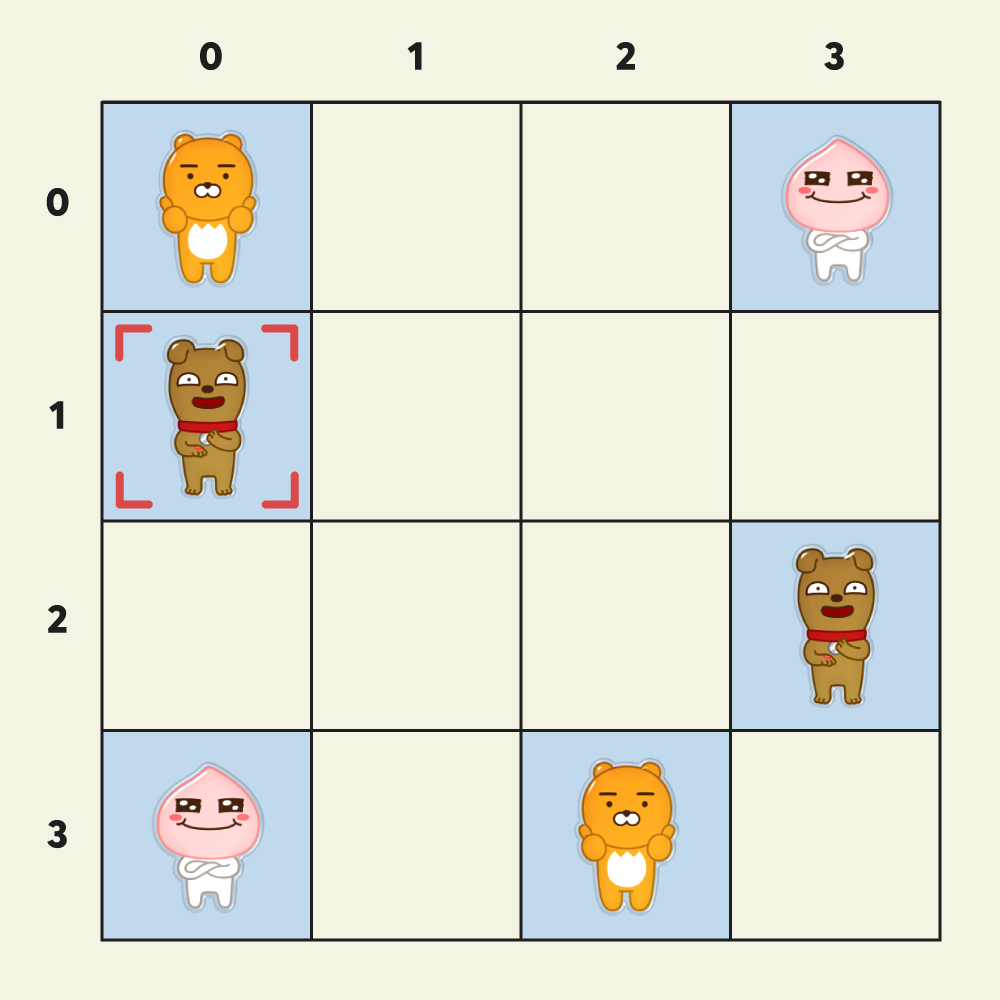
예시에서 커서는 두번째 행, 첫 번째 열 위치에서 시작하였습니다.

[Enter] 입력, ↓ 이동, [Ctrl]+→ 이동, [Enter] 입력 = 키 조작 4회
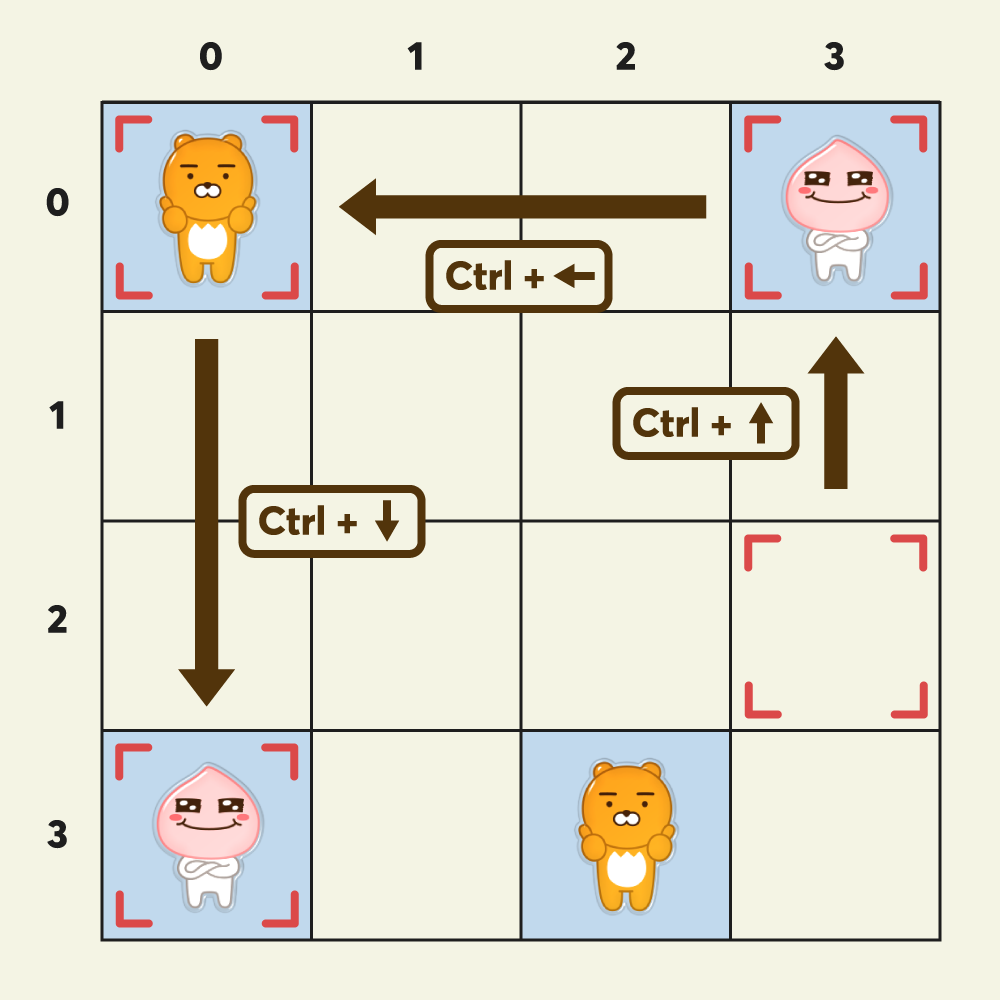
[Ctrl]+↑ 이동, [Enter] 입력, [Ctrl]+← 이동, [Ctrl]+↓ 이동, [Enter] 입력 = 키 조작 5회

[Ctrl]+→ 이동, [Enter] 입력, [Ctrl]+↑ 이동, [Ctrl]+← 이동, [Enter] 입력 = 키 조작 5회
위와 같은 방법으로 커서를 이동하여 카드를 선택하고 그림을 맞추어 카드를 모두 제거하기 위해서는 총 14번(방향 이동 8번, [Enter] 키 입력 6번)의 키 조작 횟수가 필요합니다.
현재 카드가 놓인 상태를 나타내는 2차원 배열 board와 커서의 처음 위치 r, c가 매개변수로 주어질 때, 모든 카드를 제거하기 위한 키 조작 횟수의 최솟값을 return 하도록 solution 함수를 완성해 주세요.
제한 조건
- board는 4 x 4 크기의 2차원 배열입니다.
- board 배열의 각 원소는 0 이상 6 이하인 자연수입니다.
- 0은 카드가 제거된 빈 칸을 나타냅니다.
- 1부터 6까지의 자연수는 2개씩 들어있으며 같은 숫자는 같은 그림의 카드를 의미합니다.
- 뒤집을 카드가 없는 경우(board의 모든 원소가 0인 경우)는 입력으로 주어지지 않습니다.
- r은 커서의 최초 세로(행) 위치를 의미합니다.
- c는 커서의 최초 가로(열) 위치를 의미합니다.
- r과 c는 0 이상 3 이하인 정수입니다.
- 게임 화면의 좌측 상단이 (0, 0), 우측 하단이 (3, 3)입니다.
입출력 예
| borad | r | c | result |
| [[1,0,0,3],[2,0,0,0],[0,0,0,2],[3,0,1,0]] | 1 | 0 | 14 |
| [[3,0,0,2],[0,0,1,0],[0,1,0,0],[2,0,0,3]] | 0 | 1 | 16 |
코드
#include <string>
#include <vector>
#include <queue>
#include <climits>
#include <cstring>
#include <algorithm>
#define N 4 // board의 크기 (4 X 4)
#define MAX_NUM 7 // card의 최대 길이
using namespace std;
struct pos
{
int r;
int c;
void init(int r, int c)
{
this->r = r;
this->c = c;
}
};
vector<vector<pos>> card; // card[i]는 i번 카드의 좌표
string diff_per; // 서로 다른 카드 중 어떤 것부터 뒤집을지
string same_per; // 같은 카드 중 어떤 것부터 뒤집을지 (0 or 1)
int card_num; // 존재하는 카드의 종류 (1 ~ 6)
// board를 전체적으로 확인하여 존재하는 카드와 각 카드의 좌표를 card에 저장
void init_card(vector<vector<int>> &board)
{
pos p;
int i, j;
card.clear();
card.resize(MAX_NUM);
for (i = 0; i < N; i++)
{
for (j = 0; j < N; j++)
{
if (board[i][j])
{
p.init(i, j);
card[board[i][j]].push_back(p);
}
}
}
}
// 존재하는 모든 카드의 번호를 diff_per에 추가
// 오름차순으로 저장되며 순열을 통해 모든 경우를 확인
void init_diff()
{
int i;
diff_per.clear();
for (i = 1; i < MAX_NUM; i++)
{
if (!card[i].empty())
diff_per += to_string(i);
}
}
// same_per[i]는 diff_per[i]번 카드 중 어떤 것부터 뒤집을지를 의미
// same_per[i]가 0이면 card[diff_per[i]][0]부터 뒤집고
// same_per[i]가 1이면 card[diff_per[i]][1]부터 뒤집음
// 오름차순으로 저장되며 순열을 통해 모든 경우를 확인
void init_same(int r)
{
int i;
int n = card_num;
same_per.clear();
for (i = 0; i < n - r; i++)
same_per += "0";
for (i = n - r; i < n; i++)
same_per += "1";
}
// 주어진 좌표가 board의 범위 내인지 확인
bool in_range(pos p)
{
if (p.r < 0 || p.r >= N || p.c < 0 || p.c >= N)
return false;
return true;
}
// src에서 dst로 가기 위한 최소 조작 횟수를 구함
int get_dist(pos src, pos dst, vector<vector<int>> &board)
{
queue<pos> q;
pos curr, next, tmp;
int d[] = {-1, 1, 0, 0};
bool visit[N][N];
int i, j, size;
int res = 0;
// 초기화
memset(visit, false, sizeof(visit));
// 시작점 삽입
visit[src.r][src.c] = true;
q.push(src);
// 탐색
while (!q.empty())
{
size = q.size();
for (i = 0; i < size; i++)
{
curr = q.front();
q.pop();
// 카드를 찾았으면 리턴
if (curr.r == dst.r && curr.c == dst.c)
{
return res;
}
// 방향키 이동
for (j = 0; j < 4; j++)
{
next.init(curr.r + d[j], curr.c + d[3 - j]);
if (!in_range(next) || visit[next.r][next.c])
continue;
visit[next.r][next.c] = true;
q.push(next);
}
// ctrl + 방향키 이동
for (j = 0; j < 4; j++)
{
next = curr;
while (1)
{
tmp.init(next.r + d[j], next.c + d[3 - j]);
if (!in_range(tmp))
break;
next.r += d[j];
next.c += d[3 - j];
if (board[next.r][next.c])
break;
}
if (visit[next.r][next.c])
continue;
visit[next.r][next.c] = true;
q.push(next);
}
}
// 조작 횟수 증가
res++;
}
}
// 순서에 따라 카드를 뒤집기 위한 최소 조작 횟수를 구함
int game(vector<vector<int>> board, int r, int c)
{
vector<pos> order;
pos p;
int i, j, a, b;
int res = 0;
// 최초 위치 삽입
p.init(r, c);
order.push_back(p);
// 순서에 따른 좌표 삽입
for (i = 0; i < card_num; i++)
{
a = diff_per[i] - '0';
b = same_per[i] - '0';
order.push_back(card[a][b]);
b = abs(b - 1);
order.push_back(card[a][b]);
}
// 각 좌표간 이동을 위한 최소 조작 횟수를 누적
// 두 개의 카드를 모두 뒤집은 경우 카드를 삭제 (-> 0)
// enter를 누른 횟수(2)를 더함
for (i = 1; i < order.size(); i++)
{
res += get_dist(order[i - 1], order[i], board);
if (i % 2 == 0)
{
p = order[i - 1];
board[p.r][p.c] = 0;
p = order[i];
board[p.r][p.c] = 0;
res += 2;
}
}
return res;
}
int solution(vector<vector<int>> board, int r, int c) {
int answer = INT_MAX;
int i;
init_card(board);
init_diff();
card_num = diff_per.size();
do
{
for (i = 0; i <= card_num; i++)
{
init_same(i);
do
{
// 모든 경우에 대해 최소 조작 횟수를 구해 최솟값을 갱신
answer = min(answer, game(board, r, c));
} while (next_permutation(same_per.begin(), same_per.end()));
}
} while (next_permutation(diff_per.begin(), diff_per.end()));
return answer;
}
링크
코딩테스트 연습 - 카드 짝 맞추기
[[1,0,0,3],[2,0,0,0],[0,0,0,2],[3,0,1,0]] 1 0 14 [[3,0,0,2],[0,0,1,0],[0,1,0,0],[2,0,0,3]] 0 1 16
programmers.co.kr
inbdni/Programmers
Contribute to inbdni/Programmers development by creating an account on GitHub.
github.com
'Coding Test > Programmers' 카테고리의 다른 글
| [프로그래머스] 스티커 모으기(2) / C++ (0) | 2021.03.08 |
|---|---|
| [프로그래머스] 숫자 게임 / C++ (0) | 2021.03.08 |
| [프로그래머스] 경주로 건설 / C++ (0) | 2021.03.05 |
| [프로그래머스] 기지국 설치 / C++ (0) | 2021.03.05 |
| [프로그래머스] 보석 쇼핑 / C++ (0) | 2021.03.04 |
